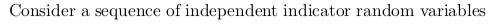
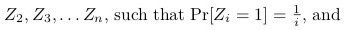
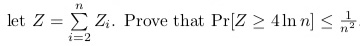
| Home Blogs | Copyright 2021, Randy Strauss |
I was afraid this was going to happen.
My older sone wanted some help with his CS homework.
He's in a PhD program...
I haven't done anything like this for 40 years.
Certainly not this. I'm sure I heard the term "Markov chain"
but I don't remember what it was.
Also, I never did much algebra with probabilities...
I used to be able to do stuff like this...
I'm guessing that an "indicator variable" is something that is boolean- just indicates that something is true.
The Z[i]'s are the value of each variable. The chance that Z[i] is true is 1/i. We can imagine each Z[i] to be an i-sided coin or dice. Imagine one side shows 'a' and all the other sides show 'b'. We roll all of the die at once. If a dice lands on 'a', it's worth one point. 'b' is worth nothing. Z is the total worth of all die together.
Imagine we use 9 die, n=9. Z[2] has a 50% chance of being 1, which is the same as saying it's chance is 1/2. Z[3] has a third of a chance, 1/3. On average we expect these 9 cubes rolled at random to be worth 1/2 + 1/3 + 1/4 + ... + 1/9. That sum happens to be about 1.83. The actual value of Z will be zero, 1, even a tiny chance of 9 if all the dice land on 'a'. But over time, the law of large numbers tells us that the average value come to about 1.83.
I'm guessing the expected value of Z is approximately ln(n),
since the integral of 1/i is the natural log.
So they want us to approximate the chance that Z will be
4 times its expected value, and show that's less than 1/(n^2).
As n goes up by 1, ln(n) goes up just a tiny bit.
From 100 to 101, ln(n) goes up by about 5/100,000, about half of 100^2.
When n goes from n to n^2, ln(n) doubles...
That sort of makes sense to me...
We could compute the value of Pr[Z > 4ln(n)]:
Let x = ceiling(4 ln(n))
I could write an algorithm that computed all the
(n-1 choose x) ways Z could end up being that big,
and compute the product of each, then add them up.
Or, estimate the average product,
and multiply that by the number of combinations...
I did a bit of searching...
Markov's inequality is that Pr[Z ≥ z] ≤ E[Z]/z
Or, substituting E[Z] = ln(n)
Pr[Z ≥ z] ≤ ln(n)/z,
substituting z = 4ln(n)
Pr[Z ≥ 4ln(n)] ≤ ln(n) / 4ln(n)
Pr[Z ≥ 4ln(n)] ≤ 1 / 4
If we run the experiment with n=5,
the expected value is (1/2)+(1/3)+(1/4)+(1/5) = 1.283.
The chance Z > 4*1.283 is zero, since with 4 variables,
Z can be at most 4.
The first one that can work is 9. 4 * ln(9) = 8.7
The chance of that is (1/2)*...*(1/10) = .000000275
For 10, 11 and 12, the log is over 9, so we'll need 10 to be true.
For 10, they all need to be true.
For 11, there are 11 ways for it to work (1/2)*...*(1/12), leaving out any one.
so that'll be about 1 less 0.
When n is large and goes from n to n+1, the expected value
only goes up a tiny bit, but there are like n more combinations
that can add up to 4*ln(n)...
Maybe we should go back to the algorithm to compute them
Say m=n-1, (m choose X) ways is m!/(X! * (m-X!))
My guess is that if I could represent the algorithm's findings as a sequence,
I could massage it a bit to make it bigger and come up with the 1/n^2...
Or, we can go back to the fact that as n goes from N to N^2, the expected value doubles. Meanwhile the chance that Z reaches that doubled value goes down by 1/4...
This is what problem solving is like- figuring out what makes sense, studying the relationships. If I were serious about this and had the time, I'd also do more research. Learning about similar systems might well find some relationships that could help. (I am not even positive that "Markov's inequality" above applies...)
Maybe next life...
PS: The next day, he emailed me the solution:
I don't know... That's all I've got for now...